Giải bài 32 SGK Toán 9 tập 2 trang 54 ✅ Vip

Sao chép

Thủ Thuật về Giải bài 32 SGK Toán 9 tập 2 trang 54 Chi Tiết

Bùi Thị Kim Oanh đang tìm kiếm từ khóa Giải bài 32 SGK Toán 9 tập 2 trang 54 được Update vào lúc : 2022-07-14 01:10:07 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha.

Bài 31 trang 54 sgk Toán 9 tập 2

Bài 31. Tính nhẩm nghiệm của những phương trình:

a) (1,5x^2-rm 1,6xrm + rm 0,1rm = rm 0);

b) (sqrt 3 x^2-rm left( 1rm - rm sqrt 3 right)xrm -rm 1rm = rm 0)

c) (left( 2rm - rm sqrt 3 right)x^2 + rm 2sqrt 3 xrm -rm left( 2rm + rm sqrt 3 right)rm = rm 0);

d) (left( mrm -rm 1 right)x^2-rm left( 2mrm + rm 3 right)xrm + rm mrm + rm 4rm = rm 0) với (m ≠ 1).
Bài giải:

a) Phương trình (1,5x^2-rm 1,6xrm + rm 0,1rm = rm 0)

Có (a + b + c = 1,5 – 1,6 + 0,1 = 0) nên (x_1 = 1;x_2 = rm 0,1 over 15 = 1 over 150)

b) Phương trình (sqrt 3 x^2-rm left( 1rm - rm sqrt 3 right)xrm -rm 1rm = rm 0)

Có (a – b + c = sqrt3 + (1 - sqrt3) + (-1) = 0) nên (x_1 = - 1,x_2 = - - 1 over sqrt 3 = rm sqrt 3 over 3)

c) (left( 2rm - rm sqrt 3 right)x^2 + rm 2sqrt 3 xrm -rm left( 2rm + rm sqrt 3 right)rm = rm 0)

Có (a + b + c = 2 - sqrt3 + 2sqrt3 – (2 + sqrt3) = 0)

Nên (x_1 = 1,x_2 = rm - (2 + sqrt 3 ) over 2 - sqrt 3 = - (2 + sqrt 3 )^2 = - 7 - 4sqrt 3 )

d) (left( mrm -rm 1 right)x^2-rm left( 2mrm + rm 3 right)xrm + rm mrm + rm 4rm = rm 0)

Có (a + b + c = m – 1 – (2m + 3) + m + 4 = 0)

Nên (x_1 = 1,x_2 = rm m + 4 over m - 1)

Bài 32 trang 54 sgk Toán 9 tập 2

Bài 32. Tìm hai số u và v trong mỗi trường hợp sau:

a) (u + v = 42), (uv = 441);

b) (u + v = -42), (uv = -400);

c) (u – v = 5), (uv = 24).

Bài giải:

a) (u + v = 42), (uv = 441) => (u, v) là nghiệm của phương trình:

(x^2-rm 42xrm + rm 441rm = rm 0)

(Delta rm = rm 21^2-rm 441rm = rm 441rm -rm 441rm = rm 0)

(rm sqrt Delta ' rm = rm 0;rm x_1 = rm x_2 = rm 21)

Vậy (u = v = 21)

b) (u + v = -42, uv = -400), (u, v) là nghiệm của phương trình:

(x^2 + rm 42xrm -rm 400rm = rm 0)

(Delta' rm = rm 441rm + rm 400rm = rm 841)

(sqrt Delta ' rm = rm 29;rm x_1 = rm 8,rm x_2 = rm - 50).

Do đó: (u = 8, v = -50) hoặc (u = -50, v = 8)

c) (u – v = 5, uv = 24). Đặt (–v = t), ta có (u + t = 5, ut = -24), ta có (u,t) là nghiệm của phương trình: (x^2 - 5x - 24 = 0)

Giải ra ta được: (x_1 = rm 8,rm x_2 = rm - 3)

Vậy (u = 8, t = -3) hoặc (u = -3, t = 8).

Do đó: (u = 8, v = 3) hoặc (u = -3, t = 8).

Bài 33 trang 54 sgk Toán 9 tập 2

Bài 33. Chứng tỏ rằng nếu phương trình (ax^2 + bx + c = 0) có nghiệm là (x_1) và (x_2) thì tam thức (ax^2 + bx + c ) phân tích được thành nhân tử như sau:

(ax^2 + rm bxrm + rm crm = rm a(xrm -rm x_1)(xrm -rm x_2)).

Áp dụng. Phân tích đa thức thành nhân tử.

a)(2x^2-rm 5xrm + rm 3)

b) (rm 3x^2 + rm 8xrm + rm 2)

Bài giải:

Biến đổi vế phải: (a(xrm -rm x_1)(xrm -rm x_2)rm = rm ax^2-rm a(x_1 + rm x_2)xrm + rm ax_1x_2)

( = ax^2 - aleft( - b over a right)x + ac over a = ax^2 + bx + c)

Vậy phương trình (ax^2 + bx + c = 0) có nghiệm là (x_1,x_2) thì:

(ax^2 + rm bxrm + rm crm = rm a(xrm -rm x_1)(xrm -rm x_2)).

Áp dụng:

a) Phương trình (2x^2-rm 5xrm + rm 3rm = rm 0) có (a + b + c = 2 – 5 + 3 = 0) nên có hai nghiệm là (x_1 = 1,x_2 = rm 3 over 2) nên:

(2x^2rm + 5x + 3 = 2(xrm - 1)(x - rm 3 over 2) = (x - 1)(2x - 3))

b) Phương trình (rm 3x^2 + rm 8xrm + rm 2) có (a = 3, b = 8, b’ = 4, c = 2).

Nên (Delta rm = rm 4^2-rm 3rm .rm 2rm = rm 10), có hai nghiệm là:

(x_1) = (frac-4 - sqrt103), (x_2)= (frac-4 + sqrt103)

nên: (3x^2 + 8x + 2 = 3(x - rm - 4 - sqrt 10 over 3)(x - rm - 4 + sqrt 10 over 3))

( = 3(x + rm 4 + sqrt 10 over 3)(x + rm 4 - sqrt 10 over 3))

Giaibaitap.me

Page 2

Bài 34 trang 56 sgk Toán 9 tập 2

Bài 34. Giải những phương trình trùng phương:

a) (x^4-rm 5x^2 + rm 4rm = rm 0);

b) (2x^4-rm 3x^2-rm 2rm = rm 0);

c) (3x^4 + rm 10x^2 + rm 3rm = rm 0)

Bài giải:

a) (x^4-rm 5x^2 + rm 4rm = rm 0)

Đặt (x^2 = rm trm ge rm 0), ta có: (t^2-rm 5trm + rm 4rm = rm 0;rm t_1 = rm 1,rm t_2 = rm 4)

Nên: (x_1 = rm - 1,rm x_2 = rm 1,rm x_3 = rm - 2,rm x_4 = rm 2).

b)(2x^4-rm 3x^2-rm 2rm = rm 0).

Đặt (x^2 = rm trm ge rm 0), ta có: (2t^2rm - 3trm - 2 = 0;t_1 = 2,t_2 = rm - 1 over 2) (loại)

Vậy:(x_1 = rm sqrt 2 ;rm x_2 = rm - sqrt 2 )

c) (3x^4 + rm 10x^2 + rm 3rm = rm 0)

Đặt (x^2 = rm trm ge rm 0), ta có:(3t^2 + 10t + 3 = 0); (t_1 = - 3) (loại), (t_2 = rm - 1 over 3) (loại).

Phương trình vô nghiệm.

Bài 35 trang 56 sgk toán 9 tập 2

Bài 35. Giải những phương trình:

a) (frac(x+ 3)(x-3)3+ 2 = x(1 - x));

b) (fracx+ 2x-5 + 3 = frac62-x);

c) (frac4x-1) = (frac-x^2-x+2(x+1)(x+2))

Bài giải:

a) (frac(x+ 3)(x-3)3+ 2 = x(1 - x))

( Leftrightarrow x^2 - 9 + 6 = 3xrm - 3x^2)

(Leftrightarrow 4x^2rm - 3xrm - 3 = 0;Delta = 57)

(x_1 = rm 3 + sqrt 57 over 8,x_2 = rm 3 - sqrt 57 over 8)

b) (fracx+ 2x-5) + 3 = (frac62-x). Điều kiện (x ≠ 2, x ≠ 5).

((x + 2)(2 – x) + 3(x – 5)(2 – x) = 6(x – 5))

( Leftrightarrow 4rm - x^2rm - 3x^2 + 21xrm - 30 = 6xrm - 30)

(Leftrightarrow 4x^2rm - 15xrm - 4 = 0,Delta = 225 + 64 = 289,sqrt Delta = 17)

(x_1 = rm - 1 over 4,x_2 = 4)

c) (frac4x-1) = (frac-x^2-x+2(x+1)(x+2)). Điều kiện: (x ≠ -1; x ≠ -2)

Phương trình tương đương:(4left( xrm + rm 2 right)rm = rm - x^2-rm xrm + rm 2)

( Leftrightarrow rm 4xrm + rm 8rm = rm 2rm -rm x^2-rm x)

( Leftrightarrow rm x^2 + rm 5xrm + rm 6rm = rm 0)

Giải ra ta được: (x_1 = rm - 2) không thỏa mãn điều kiện của ẩn nên phương trình chỉ có một nghiệm (x = -3).

Bài 36 trang 56 sgk toán 9 tập 2

Bài 36. Giải những phương trình:

a) ((3x^2-rm 5xrm + rm 1)(x^2-rm 4)rm = rm 0);

b) ((2x^2 + rm xrm -rm 4)^2-rm left( 2xrm -rm 1 right)^2 = rm 0)

Bài giải:

a) ((3x^2-rm 5xrm + rm 1)(x^2-rm 4)rm = rm 0)

( Leftrightarrow left[ matrix 3x^2 - 5x + 1 = 0 hfill cr x^2-rm 4rm = rm 0 hfill cr right. Leftrightarrow left[ matrix x = 5 pm sqrt 13 over 6 hfill cr

xrm = rm pm 2 hfill cr right.)

b) ((2x^2 + rm xrm -rm 4)^2-rm left( 2xrm -rm 1 right)^2 = rm 0)

( Leftrightarrow rm (2x^2 + rm xrm -rm 4rm + rm 2xrm -rm 1)(2x^2 + rm xrm -rm 4rm -rm 2xrm + rm 1)rm )(= rm 0)

( Leftrightarrow rm (2x^2 + rm 3xrm -rm 5)(2x^2-rm xrm -rm 3)rm = rm 0)

( Leftrightarrow left[ matrix 2x^2 + rm 3xrm -rm 5rm = rm 0 hfill cr

2x^2-rm xrm -rm 3rm = rm 0 hfill cr right.)

(x_1 = rm 1;rm x_2 = rm - 2,5;rm x_3 = rm - 1;rm x_4 = rm 1,5)

loigiaihay.com

Bài 37 trang 56 sgk Toán 9 tập 2

Bài 37. Giải phương trình trùng phương:

a) (9x^4 - 10x^2 + 1 = 0);

b) (5x^4 + 2x^2rm - 16 = 10rm - x^2);

c) (0,3x^4 + 1,8x^2 + 1,5 = 0);

d) (2x^2 + 1 = rm 1 over x^2 - 4)

Bài giải:

a) (9x^4 - 10x^2 + 1 = 0). Đặt (trm = rm x^2 ge rm 0), ta có: (9t^2-rm 10trm + rm 1rm = rm 0).

Vì (a + b + c = 9 – 10 + 1 = 0) nên (t_1 = 1,t_2 = 1 over 9)

Suy ra: (x_1 = - 1,x_2 = 1,x_3 = - 1 over 3,x_4 = rm 1 over 3)

b) (5x^4 + 2x^2rm - 16 = 10rm - x^2)

( Leftrightarrow rm 5x^4 + rm 3x^2-rm 26rm = rm 0).

Đặt (trm = rm x^2 ge rm 0), ta có: (5t^2 + rm 3trm - 26rm = rm 0)

(Delta rm = rm 9rm + rm 4rm .rm 5rm .rm 26rm = rm 529rm = rm 23^2);

(rm t_1 = rm 2,rm t_2 = rm - 2,6) (loại). Do đó: (x_1 = rm sqrt 2 ,rm x_2 = rm - sqrt 2 )

c) (0,3x^4 + 1,8x^2 + 1,5 = 0)

( Leftrightarrow rm x^4 + rm 6x^2 + rm 5rm = rm 0)

Đặt (trm = rm x^2 ge rm 0), ta có:

(t^2 + rm 6trm + rm 5rm = rm 0)

(rm t_1 = rm - 1) (loại), (rm t_2 = rm - 5) (loại).

Phương trình vô nghiệm,

Chú ý: Cũng hoàn toàn có thể nhẫn xét rằng vế trái (x^4 + rm 6x^2 + rm 5rm ge rm 5), còn vế phải bằng 0. Vậy phương trình vô nghiệm.

d) (2x^2 + 1 = rm 1 over x^2 - 4) ( Leftrightarrow 2x^2 + 5 - rm 1 over x^2 = 0).

Điều kiện (x ≠ 0)

(2x^4 + rm 5x^2-rm 1rm = rm 0). Đặt (trm = rm x^2 ge rm 0), ta có:

(2t^2 + 5trm - 1 = 0;Delta = 25 + 8 = 33),

(t_1 = rm - 5 + sqrt 33 over 4,t_2 = rm - 5 - sqrt 33 over 4) (loại)

Do đó (x_1 = rm sqrt - 5 + sqrt 33 over 2,x_2 = rm - sqrt - 5 + sqrt 33 over 2)

Giaibaitap.me

Page 3

Bài 38 trang 56 sgk Toán 9 tập 2

Bài 38. Giải những phương trình:

a) (left( xrm -rm 3 right)^2 + rm left( xrm + rm 4 right)^2 = rm 23rm -rm 3x);

b) (x^3 + rm 2x^2-rm left( xrm -rm 3 right)^2 = rm left( xrm -rm 1 right)(x^2-rm 2));

c) (left( xrm -rm 1 right)^3 + rm 0,5x^2 = rm x(x^2 + rm 1,5));

d) (fracx(x - 7)3 – 1) = (fracx2) - (fracx-43);

e) (frac14x^2-9) = (1 - frac13-x);

f) (frac2xx+1) = (fracx^2-x+8(x+1)(x-4))

Bài giải:

a) (left( xrm -rm 3 right)^2 + rm left( xrm + rm 4 right)^2 = rm 23rm -rm 3x)

( Leftrightarrow rm x^2-rm 6xrm + rm 9rm + rm x^2 + rm 8xrm + rm 16rm = rm 23rm -rm 3x)

( Leftrightarrow rm 2x^2 + rm 5xrm + rm 2rm = rm 0)

(Delta = 25rm - 16 = 9,x_1 = - 2,x_2 = - 1 over 2)

b) (x^3 + rm 2x^2-rm left( xrm -rm 3 right)^2 = rm left( xrm -rm 1 right)(x^2-rm 2))

(Leftrightarrow rm x^3 + rm 2x^2-rm x^2 + rm 6xrm -rm 9rm = rm x^3-rm x^2-rm 2xrm + rm 2)

(rm Leftrightarrow rm 2x^2 + rm 8xrm -rm 11rm = rm 0)

(Delta' = 16 + 22 = 38,x_1 = rm - 4 + sqrt 38 over 2,x_2 = - 4 - sqrt 38 over 2)

c) (left( xrm -rm 1 right)^3 + rm 0,5x^2 = rm x(x^2 + rm 1,5))

( Leftrightarrow rm x^3-rm 3x^2 + rm 3xrm -rm 1rm + rm 0,5x^2 = rm x^3 + rm 1,5x)

(Leftrightarrow rm 2,5x^2-rm 1,5xrm + rm 1rm = rm 0 Leftrightarrow rm 5x^2-rm 3xrm + rm 2rm = rm 0);

(rm Delta rm = rm 9rm -rm 40rm = rm - 31rm < rm 0)

Phương trình vô nghiệm

d) (fracx(x - 7)3– 1) = (fracx2) - (fracx-43)

( Leftrightarrow rm 2xleft( xrm -rm 7 right)rm -rm 6rm = rm 3xrm -rm 2left( xrm -rm 4 right))

(Leftrightarrow rm 2x^2-rm 14xrm -rm 6rm = rm 3xrm -rm 2xrm + rm 8)

(Leftrightarrow rm 2x^2-rm 15xrm -rm 14rm = rm 0;)

(Delta rm = rm 225rm + rm 112rm = rm 337)

(x_1 = 15 + sqrt 337 over 4,x_2 = rm 15 - sqrt 337 over 4)

e) (frac14x^2-9) = 1 - (frac13-x). Điều kiện: (xrm ne rm pm 3)

Phương trình được viết lại: (frac14x^2-9) = (1 + frac1x- 3)

( Leftrightarrow rm 14rm = rm x^2-rm 9rm + rm xrm + rm 3 )

(Leftrightarrow rm x^2 + rm xrm -rm 20rm = rm 0),

(rm Delta rm = rm 1rm + rm 4rm .rm 20rm = rm 81)

Nên (x_1 = - 1 - 9 over 2 = - 5;x_2 = - 1 + 9 over 2 = 4) (thỏa mãn)

Vậy phương trình có hai nghiệm (x_1 = rm - 5,rm x_2 = rm 4).

f) (frac2xx+1) = (fracx^2-x+8(x+1)(x-4)). Điều kiện: (x ≠ -1, x ≠ 4)

Phương trình tương đương với:

(2xleft( xrm -rm 4 right)rm = rm x^2-rm xrm + rm 8)

( Leftrightarrow rm 2x^2-rm 8xrm -rm x^2 + rm xrm -rm 8rm = rm 0)

(Leftrightarrow rm x^2-rm 7xrm -rm 8rm = rm 0)

Có (a – b + c = 1 – (-7) – 8 = 0) nên (x_1 = - 1,x_2 = 8)

Vì (x_1 = - 1)không thỏa mãn điều kiện của ẩn nên: phương trình có một nghiệm là (x = 8).

Bài 39 trang 57 sgk Toán 9 tập 2

Bài 39. Giải phương trình bằng phương pháp đưa về phương trình tích.

a) ((3x^2 - rm 7xrm -rm 10)[2x^2 + rm left( 1rm - rm sqrt 5 right)xrm + rm sqrt 5 rm -rm 3]rm = rm 0);

b) (x^3 + rm 3x^2-rm 2xrm -rm 6rm = rm 0);

c) ((x^2 - rm 1)left( 0,6xrm + rm 1 right)rm = rm 0,6x^2 + rm x);

d) ((x^2 + rm 2xrm -rm 5)^2 = rm (rm x^2-rm xrm + rm 5)^2).

Bài giải.

a) ((3x^2 - rm 7xrm -rm 10)[2x^2 + rm left( 1rm - rm sqrt 5 right)xrm + rm sqrt 5 rm -rm 3]rm = rm 0)

(Leftrightarrow)(left[ matrix (3x^2 - rm 7xrm -rm 10)rm = rm 0(1) hfill cr

2x^2 + rm left( 1rm - rm sqrt 5 right)xrm + sqrt 5 -rm 3rm = rm 0(2) hfill cr right.)

Giải (1): phương trình (a - b + c = 3 + 7 - 10 = 0)

nên (x_1 = - 1,x_2 = - - 10 over 3 = 10 over 3)

Giải (2): phương trình có (a + b + c = 2 + (1 - sqrt5) + sqrt5 - 3 = 0)

nên (x_3 = 1,x_4 = sqrt 5 - 3 over 2)

b) (x^3 + rm 3x^2-rm 2xrm -rm 6rm = rm 0) (Leftrightarrow x^2left( xrm + rm 3 right)rm -rm 2left( xrm + rm 3 right)rm = rm 0 )

(Leftrightarrow left( xrm + rm 3 right)(x^2 - rm 2)rm = rm 0)

(Leftrightarrow)(left[ matrix x + 3 = 0 hfill cr

x^2 - rm 2rm = rm 0 hfill cr right.)

Giải ra (x_1 = rm - 3,rm x_2 = rm - sqrt 2 ,rm x_3 = sqrt 2 )

c) ((x^2 - rm 1)left( 0,6xrm + rm 1 right)rm = rm 0,6x^2 + rm x) ( Leftrightarrow rm left( 0,6xrm + rm 1 right)left( x^2-rm xrm -rm 1 right)rm = rm 0)

(Leftrightarrow left[ matrix 0,6x + 1 = 0(1) hfill cr

x^2-rm xrm -rm 1rm = rm 0(2) hfill cr right.)

(1) ⇔ (0,6x + 1 = 0 )

( Leftrightarrow x_1 = - 1 over 0,6 = - 5 over 3)

(2):(Delta = ( - 1)^2 - 4.1.( - 1) = 1 + 4 = 5,sqrt Delta = sqrt 5,)

(x_2 = rm 1 - sqrt 5 over 2,x_3 = 1 + sqrt 5 over 2)

Vậy phương trình có ba nghiệm:

(x_1 = - 5 over 3,x_2 = 1 - sqrt 5 over 2,x_3 = 1 + sqrt 5 over 2),

d) ((x^2 + rm 2xrm -rm 5)^2 = rm (rm x^2-rm xrm + rm 5)^2)( Leftrightarrow rm (x^2 + rm 2xrm -rm 5)^2 - rm (rm x^2-rm xrm + rm 5)^2 = rm 0)

(Leftrightarrow (x^2 + rm 2xrm -rm 5rm + rm x^2-rm xrm + rm 5).)

((rm x^2 + rm 2xrm -rm 5rm - rm x^2 + rm xrm - rm 5)rm = rm 0)

( Leftrightarrow rm (2x^2 + rm x)left( 3xrm -rm 10 right)rm = rm 0)

⇔( x(2x + 1)(3x – 10) = 0)

Hoặc (x = 0), (x = -frac12) , (x = frac103)

Vậy phương trình có 3 nghiệm.

$$ Leftrightarrow x_1 = - 1 over 0,6 = - 5 over 3$$

Bài 40 trang 57 sgk Toán 9 tập 2

Bài 40. Giải phương trình bằng phương pháp đặt ẩn phụ:

a) (3(x^2 + rm x)^2-rm 2(x^2 + rm x)rm -rm 1rm = rm 0);

b) ((x^2-rm 4xrm + rm 2)^2 + rm x^2-rm 4xrm -rm 4rm = rm 0);

c) (x - sqrtx = 5sqrtx + 7);

d) (fracxx+ 1 – 10 . fracx+1x= 3)

Hướng dẫn: a) Đặt (trm = rm x^2 + rm x), ta có phương trình (3t^2-rm 2trm - rm 1rm = rm 0). Giải phương trình này, ta tìm được hai giá trị của (t). Thay mỗi giá trị của (t) vừa tìm được vào đằng thức (trm = rm x^2 + rm x) , ta được một phương trình của ẩn (x). Giải mỗi phương trình này sẽ tìm được giá trị của (x).

d) Đặt (fracx+1x = t) hoặc (fracxx+ 1 = t)

Bài giải:

a) (3(x^2 + rm x)^2-rm 2(x^2 + rm x)rm -rm 1rm = rm 0). Đặt (trm = rm x^2 + rm x), ta có:

(3t^2rm - 2trm - 1 = 0;t_1 = 1,t_2 = - 1 over 3)

Với (t_1 = 1), ta có: (x^2 + rm xrm = rm 1rm ) hay (rm x^2 + rm xrm -rm 1rm = rm 0,Delta rm = 4rm + rm 1rm = 5,rm sqrt Delta = sqrt 5 )

(x_1 = - 1 + sqrt 5 over 2,x_2 = - 1 - sqrt 5 over 2)

Với (t_2= -frac13), ta có: (x^2 + x = - 1 over 3)hay (3x^2 + 3xrm + 1rm = 0):

Phương trình vô nghiệm, vì (Delta = 9 – 4 . 3 . 1 = -3 < 0)

Vậy phương trình đã cho có hai nghiệm: (x_1 = - 1 + sqrt 5 over 2,x_2 = - 1 - sqrt 5 over 2)

b) ((x^2-rm 4xrm + rm 2)^2 + rm x^2-rm 4xrm -rm 4rm = rm 0)

Đặt (trm = rm x^2-rm 4xrm + rm 2), ta có phương trình (t^2 + rm trm -rm 6rm = rm 0)

Giải ra ta được (t_1 = rm 2,rm t_2 = rm - 3).

- Với (t_1= 2) ta có: (x^2-rm 4xrm + rm 2rm = rm 2) hay (x^2-rm 4xrm = rm 0). Suy ra (x_1 = rm 0,rm x_2 = rm 4).

- Với (t_2= -3), ta có: (x^2-rm 4xrm + rm 2rm = rm - 3) hay (x^2-rm 4xrm + rm 5rm = rm 0).

Phương trình này vô nghiệm vì (Delta= (-4)^2 – 4 . 1 . 5 = 16 – 20 = -4 < 0)

Vậy phương trình đã cho có hai nghiệm: (x_1 = 0, x_2= 4).

c) (x - sqrtx = 5sqrtx + 7). Điều kiện: (x ≥ 0). Đặt (t = sqrtx, t ≥ 0)

Ta có:(t^2-rm 6trm -rm 7rm = rm 0). Suy ra: (t_1= -1) (loại), (t_2= 7)

Với (t = 7), ta có: (sqrtx = 7). Suy ra (x = 49).

Vậy phương trình đã cho có một nghiệm: (x = 49)

d) (fracxx+ 1– 10 . fracx+1x = 3). Điều kiện: (x ≠ -1, x ≠ 0)

Đặt (fracxx+ 1) = t, ta có: (fracx+1x) = (frac1t). Vậy ta có phương trình: (t - frac10t – 3 = 0)

hay: (t^2-rm 3trm -rm 10rm = rm 0). Suy ra (t_1 = 5, t_2 = -2).

- Với (t_1= 5), ta có (fracxx+ 1 = 5) hay (x = 5x + 5). Suy ra (x = -frac54)

- Với (t_2 = -2), ta có (fracxx+ 1= -2) hay (x = -2x – 2). Suy ra (x = -frac23).

Vậy phương trình đã cho có hai nghiệm: (x_1= -frac54), (x_2 =-frac23)

Giaibaitap.me

Page 4

Bài 41 trang 58 sgk Toán 9 tập 2

Bài 41. Trong lúc học nhóm bạn Hùng yêu cầu bạn Minh và bạn Lan từng người chọn một số trong những sao cho hai số này hơn kém nhau là 5 và tích của chúng phải bằng 150. Vậy hai bạn Minh và Lan phải chọn những số nào ?

Bài giải.

Gọi số mà một bạn đã chọn là: (x) và số bạn kia chọn là: (x+5).

Tích của hai số là: (x(x+5))

Theo đầu bài ta có phương trình:

(x(x+5)=150) hay (x^2+5x-150=0)

Giải phương trình ta được: (x_1=10,x_2=-15)

Vậy:+) nếu bạn Minh chọn số 10 thì bạn Lan chọn số 15 hoặc ngược lại.

+) nếu bạn Minh chọn số -15 thì bạn Lan chọn số -10 hoặc ngược lại.

Bài 42 trang 58 sgk Toán 9 tập 2

Bài 42. Bác Thời vay 2 000 000 đồng của ngân hàng nhà nước để làm kinh tế tài chính mái ấm gia đình trong thời hạn một năm. Lẽ ra thời điểm ở thời điểm cuối năm bác phải trả cả vốn lẫn lãi, song bác đã được ngân hàng nhà nước cho kéo dãn thời hạn thêm một năm nữa, số lãi của năm đầu được gộp vào với vốn để tính lãi năm sau và lãi suất vay vẫn như cũ. Hết hai năm bác phải trả tất cả là 2 420 000 đồng. Hỏi lãi suất vay cho vay vốn là bao nhiêu phần trăm trong một năm ?

Bài giải:

Gọi lãi suất vay cho vay vốn là (x) (%), ((x > 0)).

Tiền lãi sau một năm là: (2 000 000 . fracx100) hay (20000x) (đồng)

Sau 1 năm cả vốn lẫn lãi sẽ là: (2 000 000 + 20000x) (đồng)

Tiền lãi riêng năm thứ hai phải chịu là:

((2 000 000 + 20000x)fracx100)hay (20000x + 200x^2)

Số tiền sau hai năm bác Thời phải trả là:

(2 000 000 + 40000x + 200x^2)

Theo đầu bài ra ta có phương trình:

(2 000 000 + 40 000x + 200x^2= 2 420 000)

hay (x^2+ 200x - 2 100 = 0)

Giải phương trình:

(Delta = 100^2 - 1 . (-2 100) = 10 000 + 2 100 = 12 100)

(=> sqrtDelta'= 110)

nên (x_1) = (frac-100-1101 = -210), (x_2)= (frac-100+1101= 10)

Vì (x > 0) nên (x_1) không thỏa mãn điều kiện của ẩn.

Vậy lãi suất vay là 10%.

Bài 43 trang 58 sgk Toán 9 tập 2

Bài 43. Một xuồng du lịch đi từ thành phố Cà Mau đến Đất Mũi theo một đường sông dài (120) km. Trên đường đi, xuồng có nghỉ lại 1 giờ ở thị trấn Năm Căn. Khi về, xuồng đi theo đường dài hơn thế nữa đường lúc đi (5)km và với vận tốc nhỏ hơn vận tốc lúc đi là (5) km/h. Tính vận tốc của xuồng lúc đi, biết rằng thời gian về bằng thời gian đi.

Bài giải:

Gọi vận tốc của xuồng lúc đi là (x)(km/h), (x > 0), thì vân tốc lúc về là (x - 5) (km/h).

Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là: (frac120x + 1) (giờ)

Đường về dài: (120 + 5 = 125) (km)

Thời gian về là: (frac125x-5) (giờ)

Theo đầu bài có phương trình: (frac120x + 1 =frac125x-5)

Giải phương trình:

(x^2 – 5x + 120x – 600 = 125x Leftrightarrow x^2 – 10x – 600 = 0)

∆’ = (-5)2 – 1 . (-600) = 625, √∆’ = 25

(x_1 = 5 – 25 = -20, x_2 = 5 + 25 = 30)

Vì (x > 0) nên (x_1 = -20) không thỏa mãn điều kiện của ẩn.

Vậy vận tốc của xuồng khi đi là 30 km/h

Bài 44 trang 58 sgk Toán 9 tập 2

Bài 44. Đố em vừa tìm được một số trong những mà một nửa của nó trừ đi một nửa đơn vị rồi nhân với một nửa của nó bằng một đơn vị.

Giải

Gọi số phải tìm là (x).

Theo giả thiết một nửa của nó trừ đi một nửa đơn vị là: (fracx2) - (frac12)

Theo đầu bài ta có phương trình: ((fracx2-frac12))(fracx2) = (frac12)

hay (x^2 – x – 2 = 0), có (a – b + c = 1 – (-1) – 2 = 0) nên: (x_1 = -1, x_2 = 2)

Vậy số phải tìm bằng -1 hoặc 2.

Giaibaitap.me

Page 5

Bài 45 trang 59 sgk Toán 9 tập 2

Bài 45. Tích của hai số tự nhiên liên tục to hơn tổng của chúng là 109. Tìm hai số đó.

Bài giải:

Gọi số bé là (x), (x ∈ N, x > 0),

số tự nhiên kề sau là (x + 1).

Tích của hai số này là (x(x + 1)) hay (x^2+ x).

Theo đầu bài ta tích của hai số to hơn tổng của chúng là 109 nên ta có phương trình:

(x^2 + x - 2x - 1 = 109) hay (x^2- x - 110 = 0)

Giải phương trình: (Delta = 1 + 440 = 441), (sqrtDelta = 21)

(x_1 = 11, x_2 = -10)

Vì (x > 0) nên (x_2 = -10) không thỏa mãn điều kiện của ẩn.

Vậy hai số phải tìm là: 11 và 12

Bài 46 trang 59 sgk Toán 9 tập 2

Bài 46. Một mảnh đất nền hình chữ nhật có diện tích s quy hoạnh (240) mét vuông. Nếu tăng chiều rộng (3) m và giảm chiều dài (4) m thì diện tích s quy hoạnh mảnh đất nền không đổi. Tính kích thước của mảnh đất nền.

Bài giải:

Gọi chiều rộng của mảnh đất nền là (x) (m), (x > 0).

Vì diện tích s quy hoạnh của mảnh đất nền bằng (240) mét vuông nên chiều dài là: (frac240x) (m)

Nếu tăng chiều rộng (3)m và giảm chiều dài (4)m thì mảnh đất nền mới có chiều rộng là (x + 3) (m),

chiều dài là ((frac240x- 4)) (m) và diện tích s quy hoạnh là:

((x + 3)(frac240x) - 4) ( mét vuông )

Theo đầu bài ta có phương trình: ((x + 3)(frac240x- 4) = 240)

Từ phương trình này suy ra:

(-4x^2 – 12x + 240x + 720 = 240x)

hay (x^2 + 3x – 180 = 0)

Giải phương trình: (Delta = 3^2 + 720 = 729), (sqrtDelta = 27)

(x_1 = 12, x_2 = -15)

Vì (x > 0) nên (x_2 = -15) không thỏa mãn điều kiện của ẩn. Do đó chiều rộng là (12)m, chiều dài là: (240 : 12 = 20) (m)

Vậy mảnh đất nền có chiều rộng là (12)m, chiều dài là (20)m.

Bài 47 trang 59 sgk Toán 9 tập 2

Bài 47. Bác Hiệp và cô Liên đi xe đạp từ làng lên tỉnh trên quãng đường dài (30) km, khởi hành cùng một lúc. Vận tốc xe của bác Hiệp to hơn vận tốc xe của cô Liên là (3) km/h nên bác Hiệp đã đến tỉnh sớm hơn cô Liên nửa giờ. Tính vận tốc xe từng người.

Bài giải:

Gọi vận tốc của bác Hiệp là (x) (km/h), (x > 0) khi đó vận tốc của cố Liên là (x - 3) (km/h)

Thời gian bác Hiệp đi từ làng lên tỉnh là (frac30x) (giờ).

Thời gian bác Liên đi từ làng lên tỉnh là: (frac30x-3) (giờ)

Vì bác Hiệp đến trước cô Liên nửa giờ, tức là thời gian đi của bác Hiệp ít hơn thời gian cô Liên nửa giờ nên ta có phương trình:

(frac30x-3) - (frac30x) = (frac12)

Giải phương trình:

(x(x - 3) = 60x - 60x + 180) hay (x^2 – 3x - 180 = 0)

(x_1 = 15, x_2 = -12)

Vì (x > 0 )nên (x_2 = -12) không thỏa mãn điều kiện của ẩn.

Vậy vận tốc của bác Hiệp là (15) km/h

Vận tốc của cô Liên là )12) km/h

Giaibaitap.me

Page 6

Bài 48 trang 59 sgk Toán 9 tập 2

Bài 48. Từ một miếng tôn hình chữ nhật người ta cắt ở bốn góc bốn hình vuông vắn có cạnh bằng (5) dm để làm thành một chiếc thùng hình hộp chữ nhật không nắp có dung tích (1500) dm3 (h.15). Hãy tính kích thước của miếng tôn lúc đầu, biết rằng chiều dài của nó gấp hai chiều rộng.

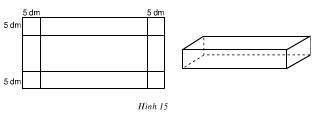
Bài giải:

Gọi chiều rộng của miếng tôn là (x) (dm), (x > 0).

Chiều dài của nó là (2x) (dm)

Khi làm thành một chiếc thùng không đáy thì chiều dài của thùng là (2x - 10) (dm), chiều rộng là (x - 10) (dm), độ cao là (5) (dm).

Dung tích của thùng là (5(2x - 10)(x - 10)) (dm3)

Theo đầu bài ta có phương trình:

(5(2x - 10)(x - 10) = 1500) hay

(x^2 – 15x – 100 = 0)

Giải phương trình: (Delta = 225 + 400 = 625), (sqrtDelta = 25)

(x_1 = 20, x_2 = -5) (loại)

Vậy miếng tôn có chiều rộng bằng 20 (dm), chiều dài bằng 40 (dm).

Bài 49 trang 59 sgk Toán 9 tập 2

Bài 49. Hai đội thợ quét sơn một ngôi nhà. Nếu họ cùng làm thì trong 4 ngày xong việc. Nếu họ làm riêng thì đội I hoàn thành xong việc làm nhanh hơn đội II là 6 ngày. Hỏi nếu làm riêng thì mỗi đội phải làm trong bao nhiêu ngày để xong việc ?

Bài giải:

Gọi thời gian đội I làm một mình xong việc là (x) (ngày), (x > 0).

Vì đội II hoàn thành xong việc làm lâu hơn đội I là 6 ngày nên thời gian một mình đội II làm xong việc là (x + 6) (ngày).

Mỗi ngày đội I làm được (frac1x) (việc làm).

Mỗi ngày đội II làm được (frac1x+6) (việc làm)

Hai đội làm 4 ngày xong việc làm ra mỗi ngày cả hai đội làm được (frac14) việc làm ta có phương trình:

(frac1x) + (frac1x+6) = (frac14)

Giải phương trình: (x(x + 6) = 4x + 4x + 24) hay (x^2– 2x - 24 = 0), (Delta' = 1 + 24 = 25 = 5^2)

(x_1 = 1 + 5 = 6, x_2 = 1 - 5 = -4)

Vì (x > 0) nên (x_2 = 1 - 5 = -4) không thỏa mãn điều kiện của ẩn.

Vậy một mình đội I làm trong (6) ngày thì xong việc.

Một mình đội II làm trong (12) ngày thì xong việc.

Bài 50 trang 59 sgk Toán 9 tập 2

Bài 50. Miếng sắt kẽm kim loại thứ nhất nặng (880) g, miếng sắt kẽm kim loại thứ hai nặng (858) g. Thể tích của miếng thứ nhất nhỏ hơn thể tích của miếng thứ hai là (10) cm3, nhưng khối lượng riêng của miếng thứ nhất to hơn khối lượng riêng của miếng thứ hai là (1) g/cm3 . Tìm khối lượng riêng của mỗi miếng sắt kẽm kim loại.

Bài giải:

Gọi khối lượng riêng của miếng sắt kẽm kim loại thứ nhất là: (x) (g/cm3 )

Khối lượng riêng của miếng sắt kẽm kim loại thứ hai là: (x - 1) (g/cm3 )

Thể tích của miếng sắt kẽm kim loại thứ nhất là: (frac880x) (cm3 )

Thể tích của miếng sắt kẽm kim loại thứ hai là: (frac858x-1) (cm3 )

Theo đầu bài thể tích của miếng thứ nhất nhỏ hơn miếng thứ hai là (10) cm3 nên ta có phương trình: (frac858x-1 - frac880x = 10)

Giải phương trình:

(10x(x - 1) = 858x - 880x + 880) hay (5x^2 + 6x - 440 = 0)

(Delta'=9 + 2200 = 2209), (sqrtDelta' = 47)

(x_1= 8,8, x_2 = -10)

Vì (x > 0) nên (x_2 = -10) (loại)

Vậy khối lượng riêng của miếng sắt kẽm kim loại thứ nhất là: (8,8) g/cm3

Khối lượng riêng của miếng sắt kẽm kim loại thứ hai là: (7,8) g/cm3

Giaibaitap.me

Page 7

Bài 51 trang 59 sgk Toán 9 tập 2

Bài 51. Người ta đổ thêm (200) g nước vào một dung dịch chứa (40) g muối thì nồng độ của dung dịch giảm sút (10) %. Hỏi trước khi đổ thêm nước thì dung dịch chứa bao nhiêu nước ?

Bài giải:

Gọi trọng lượng nước trong dung dịch trước khi đổ thêm nước là: (x) (g), (x > 0)

Nồng độ muối của dung dịch khi đó là: (frac40x + 40)

Nếu đổ thêm (200) g nước vào dung dịch thì trọng lượng của dung dịch sẽ là: (x + 40 + 200) (g)

Nồng độ của dung dịch giờ đây là: (frac40x + 240)

Vì nồng độ muối giảm (10)% nên ta có phương trình:

(frac40x + 40) - (frac40x + 240) = (frac10100)

Giải phương trình:

((x + 40)(x + 240) = 400(x + 240 - x - 40))

hay (x^2 + 280x - 70400 = 0)

(Delta' = 19600 + 70400 = 90000), (sqrtDelta' = 300)

(x_1 = 160, x_2 = -440)

Vì (x > 0) nên (x_2 = -440) (loại)

Vậy trước khi đổ thêm nước, trong dung dịch có (160) g nước.

Bài 52 trang 60 sgk Toán 9 tập 2

Bài 52. Khoảng cách giữa hai bên sông A và B là (30) km. Một canô đi từ bến A đến bến B, nghỉ (40) phút ở bến B rồi quay lại bến A. Kể từ lúc khởi hành đến khi về tới bến A hết tất cả (6) giờ. Hãy tìm vận tốc của canô trong nước yên lặng, biết rằng vận tốc của nước chảy là (3) km/h.

Bài giải:

Gọi vận tốc thực của canô là (x) (km/h), (x > 3) , nên vận tốc khi đi xuôi dòng là: (x + 3) (km/h) và vận tốc khi ngược dòng là: (x - 3) (km/h)

Thời gian xuôi dòng là: (frac30x + 3) (giờ)

Thời gian ngược dòng là: (frac30x - 3) (giờ)

Nghỉ lại (40) phút hay (frac23) giờ ở B.

Theo đầu bài Tính từ lúc lúc khời hành đến khi về tới bến A hết tất cả (6) giờ nên ta có phương trình: (frac30x+ 3+ frac30x- 3+ frac23 = 6)

Giải phương trình:

(16(x + 3)(x - 3) = 90(x + 3 + x - 3)) hay: (4x^2 - 45x - 36 = 0)

(Delta = 2025 + 576 = 2601, sqrtDelta = 51)

(x_1 = 12, x_2 = -frac34) (loại)

Vậy vận tốc của canô trong nước yên lặng là (12) km/h.

Bài 53 trang 60 sgk Toán 9 tập 2

Bài 53. Tỉ số vàng. Đố em chia được đoan AB cho trước thành hai đoạn sao cho tỉ số giữa đoạn lớn với đoạn AB bằng tỉ số giữa đoạn nhỏ với đoạn lớn (h.16).

Hãy tìm tỉ số ấy.

Đó đó đó là bài toán mà Ơ-clít đưa ra từ thế kỉ III trước công nguyên. Tỉ số nói trong bài toán được gọi là tỉ số vàng, còn phép chia nói trên được gọi là phép chia vàng hay phép chia hoàng kim.

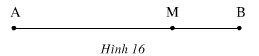
Hướng dẫn: Giả sử M là vấn đề chia và AM > MB. Gọi tỉ số cần tìm là (x).

Bài giải:

Giả sử(M) là vấn đề chia đoạn (AB) và (AB) có độ dài bằng (a).

Gọi độ dài của (AM = x, 0 < x < a). Khi đó (MB = a - x).

Theo đầu bài: (AM over AB = MB over AM) hay (x over a = a - x over x)

Giải phương trình: (x^2 = a(a - x)) hay (x^2 + ax - a^2= 0)

(Delta = a^2 + 4a^2= 5a^2 , sqrtDelta= asqrt5)

(x_1 = - a + asqrt 5 over 2 = a(sqrt 5 - 1) over 2,x_2 = - a(sqrt 5 + 1) over 2)

Vì (x > 0) nên (x_2) không thỏa mãn điều kiện của ẩn.

Vậy (AM=a(sqrt 5 - 1) over 2)

Tỉ số cần tìm là: (AM over AB = sqrt 5 - 1 over 2)

Giaibaitap.me

Page 8

Bài 54 trang 63 SGK Toán 9 tập 2

Bài 54. Vẽ đồ thị của hàm số (y = 1 over 4x^2) và (y = - 1 over 4x^2) trên cùng một hệ trục tọa độ

a) Qua điểm (B(0; 4)) kẻ đường thẳng song song với trục Ox. Nó cắt đồ thị của hàm số (y = 1 over 4x^2) tại hai điểm M và M’. Tìm hoành độ của M và M’.

b) Tìm trên đồ thị của hàm số (y = - 1 over 4x^2) điểm N có cùng hoành độ với M, điểm N’ có cùng hoành độ với M’. Đường thẳng NN’ có song song với Ox không? Vì sao? Tìm tung độ của N và N’ bằng hai cách:

- Ước lượng trên hình vẽ:

- Tính toán theo công thức.

Giải:

Vẽ đồ thị hàm số:

* Hàm số (y = 1 over 4x^2) và (y = - 1 over 4x^2)

- Tập xác định (D = R)

- Bảng giá trị

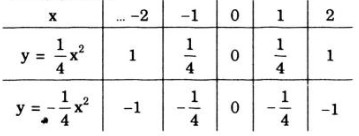
- Đồ thị hàm số (y = 1 over 4x^2) và (y = - 1 over 4x^2) là những Parabol có đỉnh là gốc tọa độ O và nhận Oy làm trục đối xứng. Đồ thị hàm số (y = 1 over 4x^2) nằm trên trục hoành, đồ thị hàm số (y = - 1 over 4x^2) nằm dưới trục hoành.

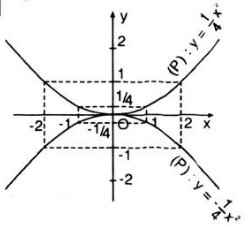
a) Đường thẳng qua (B(0; 4)) song song với (Ox) cắt đồ thị tại hai điểm (M, M') (xem trên đồ thị). Từ đồ thị ta có hoành độ của (M) là (x = 4), của (M') là (x = - 4).

b) Trên đồ thị hàm số (y = - 1 over 4x^2) ta xác định được điểm (N) và (N’) có cùng hoành độ với (M, M’). ta được đường thẳng (M, M’)

Tìm tung độ của (N, N’)

- Ước lượng trên hình vẽ được tung độ của (N) là (y = - 4); của (N’) là (y = -4)

- Tính toán theo công thức:

Điểm (N) trên (y = - 1 over 4x^2) có (x = 4) nên (y = - 1 over 4.4^2 = - 4)

Điểm (N’) trên (y = - 1 over 4x^2) có (x = 4) nên (y = - 1 over 4.( - 4)^2 = - 4)

Vậy tung độ của (N, N’ = -4).

Bài 55 trang 63 SGK Toán 9 tập 2

Bài 55. Cho phương trình (x^2 – x – 2 = 0)

a) Giải phương trình

b) Vẽ hai đồ thị (y = x^2) và (y = x + 2) trên cùng một hệ trục tọa độ.

c) Chứng tỏ rằng hai nghiệm tìm được trong câu a) là hoành độ giao điểm của hai đồ thị.

Hướng dẫn làm bài:

a) Giải phương trình: (x^2 – x – 2 = 0)

(Delta = (-1)^2– 4.1.(-2) = 1 + 8 > 0)

(sqrtDelta= sqrt9 = 3)

(Rightarrow x_1 = -1; x_2= 2)

b) Vẽ đồ thị hàm số

- Hàm số (y = x^2)

+ Bảng giá trị:

- Hàm số (y = x + 2)

+ Cho (x = 0 ⇒ y = 2) được điểm (A(0;2))

+ Cho (x = -2 ⇒ y = 0) được điểm (B(-2;0))

Đồ thị hàm số:

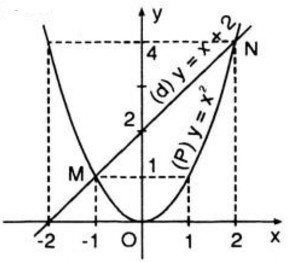
c) Ta có phương trình hoành độ giao điểm của hai đồ thị là:

(x^2 = x + 2 Leftrightarrow x^2 - x - 2 = 0 Leftrightarrow left{ matrixx_1 = - 1 hfill cr x_2 = 2 hfill cr right.)

Điều này chứng tỏ rằng đồ thị đường thẳng cắt đồ thị parapol tại hai điểm có hoành độ lần lượt là (x = -1; x= 2). Hai giá trị này cũng đó đó là nghiệm của phương trình (x^2 - x - 2 = 0) ở câu a).

Bài 56 trang 63 SGK Toán 9 tập 2

Bài 56. Giải những phương trình:

a) (3rmx^4 - 12rmx^2 + 9 = 0)

b) (2rmx^4 + 3rmx^2 - 2 = 0)

c) (x^4 + 5rmx^2 + 1 = 0)

Hướng dẫn làm bài:

a) (3rmx^4 - 12rmx^2 + 9 = 0)

Đặt (t = x^2left( t ge 0 right))

Ta có phương trình:

(eqalign & 3t^2 - 12t + 9 = 0 cr

& Leftrightarrow t^2 - 4t + 3 = 0 cr )

Phương trình có (a + b + c = 0) nên có hai nghiệm (t_1 = 1; t_2 = 3) (đều thỏa mãn)

Với (t_1 = 1 Rightarrow x^2 = 1 Leftrightarrow x = pm 1)

Với (t_2 = 3 Rightarrow x^2 = 3 Leftrightarrow x = pm sqrt 3)

b) (2rmx^4 + 3rmx^2 - 2 = 0)

Đặt (t = x^2left( t ge 0 right))

Ta có phương trình :

(eqalign & 2t^2 + 3t - 2 = 0 cr & Delta = 9 + 16 = 25 Rightarrow sqrt Delta = 5 cr

& Rightarrow t_1 = - 3 + 5 over 4 = 1 over 2(TM);t_2 = - 2(loại) cr)

Với (t = 1 over 2 Rightarrow x^2 = 1 over 2 Leftrightarrow x = pm sqrt 1 over 2 = pm sqrt 2 over 2)

c) (x^4 + 5rmx^2 + 1 = 0)

Đặt (t = x^2left( t ge 0 right))

Ta có phương trình :

(t^2 + 5t + 1 = 0)

(Delta = 25 – 2 = 21)

(eqalign & Rightarrow t_1 = - 5 + sqrt 21 over 2 < 0(loại) cr

& t_2 = - 5 - sqrt 21 over 2 < 0(loại) cr )

Vậy phương trình vô nghiệm

Bài 57 trang 63 SGK Toán 9 tập 2

Bài 57. Giải những phương trình:

a) (5rmx^2 - 3rmx + 1 = 2rmx + 11)

b) (x^2 over 5 - 2rmx over 3 = x + 5 over 6)

c) (x over x - 2 = 10 - 2rmx over x^2 - 2rmx)

d) (x + 0,5 over 3rmx + 1 = 7rmx + 2 over 9rmx^2 - 1)

e) (2sqrt 3 x^2 + x + 1 = sqrt 3 left( x + 1 right))

f) (x^2 + 2sqrt 2 x + 4 = 3left( x + sqrt 2 right))

Hướng dẫn làm bài:

(eqalign & 5rmx^2 - 3rmx + 1 = 2rmx + 11 cr & Leftrightarrow 5rmx^2 - 5rmx - 10 = 0 cr

& Leftrightarrow x^2 - x - 2 = 0 cr)

Phương trình có (a – b + c = 1 + 1 – 2 = 0) nên có 2 nghiệm (x_1= -1; x_2= 2)

(eqalign & x^2 over 5 - 2rmx over 3 = x + 5 over 6 cr & Leftrightarrow 6rmx^2 - 20rmx = 5rmx + 25 cr & Leftrightarrow 6rmx^2 - 25rmx - 25 = 0 cr & Delta = 25^2 + 4.6.25 = 1225 cr

& sqrt Delta = 35 Rightarrow x_1 = 5;x_2 = - 5 over 6 cr )

c) (x over x - 2 = 10 - 2rmx over x^2 - 2rmx) ĐKXĐ: (x ≠ 0; x ≠ 2)

(eqalign & Leftrightarrow x^2 = 10 - 2rmx cr & Leftrightarrow x^2 + 2rmx - 10 = 0 cr & Delta ' = 1 + 10 = 11 cr & Rightarrow x_1 = - 1 + sqrt 11 (TM) cr

& x_2 = - 1 - sqrt 11 (TM) cr )

d) (x + 0,5 over 3rmx + 1 = 7rmx + 2 over 9rmx^2 - 1) ĐKXĐ: (x ne pm 1 over 3)

(eqalign & Leftrightarrow 2rmx + 1 over 3rmx + 1 = 14rmx + 4 over 9rmx^2 - 1 cr & Leftrightarrow left( 2rmx + 1 right)left( 3rmx - 1 right) = 14rmx + 4 cr & Leftrightarrow 6rmx^2 + x - 1 = 14rmx + 4 cr & Leftrightarrow 6rmx^2 - 13rmx - 5 = 0 cr & Delta = ( - 13)^2 - 4.6.( - 5) = 289 cr & sqrt Delta = sqrt 289 = 17 cr & Rightarrow x_1 = 5 over 2(TM) cr

& x_2 = - 1 over 3(loại) cr )

(eqalign & 2sqrt 3 x^2 + x + 1 = sqrt 3 left( x + 1 right) cr & Leftrightarrow 2sqrt 3 x^2 - left( sqrt 3 - 1 right)x + 1 - sqrt 3 = 0 cr & Delta = left( sqrt 3 - 1 right)^2 - 8sqrt 3 left( 1 - sqrt 3 right) cr & = 15 - 2.5.sqrt 3 + 3 = left( 5 - sqrt 3 right)^2 cr & sqrt Delta = sqrt left( 5 - sqrt 3 right)^2 = 5 - sqrt 3 cr & Rightarrow x_1 = sqrt 3 - 1 + 5 - sqrt 3 over 4sqrt 3 = sqrt 3 over 3 cr

& x_2 = sqrt 3 - 1 - 5 + sqrt 3 over 4sqrt 3 = 1 - sqrt 3 over 2 cr)

(eqalign & x^2 + 2sqrt 2 x + 4 = 3left( x + sqrt 2 right) cr & Leftrightarrow x^2 + left( 2sqrt 2 - 3 right)x + 4 - 3sqrt 2 = 0 cr & Delta = 8 - 12sqrt 2 + 9 - 16 + 12sqrt 2 = 1 cr & sqrt Delta = 1 cr & Rightarrow x_1 = 3 - 2sqrt 2 + 1 over 2 = 2 - sqrt 2 cr

& x_2 = 3 - 2sqrt 2 - 1 over 2 = 1 - sqrt 2 cr )

Giaibaitap.me

Page 9

Bài 58 trang 63 SGK Toán 9 tập 2

Bài 58. Giải những phương trình

a) (1,2rmx^3 - x^2 - 0,2rmx = 0)

b) (5rmx^3 - x^2 - 5rmx + 1 = 0)

Hướng dẫn làm bài:

a) (1,2rmx^3 - x^2 - 0,2rmx = 0) (1)

( Leftrightarrow xleft( 1,2rmx^2 - x - 0,2 right) = 0)

(Leftrightarrow left[ matrixx = 0 hfill cr1,2rmx^2 - x - 0,2 = 0(*) hfill cr right.)

Giải (*): (1,2x^2 – x – 0,2 = 0)

Ta có: (a + b + c = 1,2 + (-1) + (-0,2) = 0)

Vậy (*) có 2 nghiệm: (x_1= 1); (x_2 = - 0,2 over 1,2 = - 1 over 6)

Vậy phương trình đã cho có 3 nghiệm: (x_1 = 0;x_2 = 1;x_3 = - 1 over 6)

b) (5rmx^3 - x^2 - 5rmx + 1 = 0)

(⇔ x^2(5x – 1) – (5x – 1) = 0)

(⇔ (5x – 1)(x^2– 1) = 0)

( Leftrightarrow left[ matrix5rmx - 1 = 0 hfill cr x^2 - 1 = 0 hfill cr right. Leftrightarrow left[ matrixx = 1 over 5 hfill cr x = pm 1 hfill cr right.)

Vậy phương trình (2) có 3 nghiệm: (x_1 = 1 over 5;x_2 = - 1;x_3 = 1)

Bài 59 trang 63 SGK Toán 9 tập 2

Bài 59. Giải những phương trình bằng phương pháp đặt ẩn phụ:

a) (2left( x^2 - 2rmx right)^2 + 3left( x^2 - 2rmx right) + 1 = 0)

b) (left( x + 1 over x right)^2 - 4left( x + 1 over x right) + 3 = 0)

Hướng dẫn làm bài:

a) (2left( x^2 - 2rmx right)^2 + 3left( x^2 - 2rmx right) + 1 = 0)

Đặt (x^2 – 2x = t). Khi đó (1) (⇔ 2t^2+ 3t +1 = 0 )(*)

Phương trình (*) có (a – b + c = 2 – 3 + 1 = 0)

Vậy phương trình (*) có hai nghiệm:

- Với (t = -1). Ta có

(eqalign & x^2 - 2rmx = - 1 Leftrightarrow x^2 - 2rmx + 1 = 0 cr

& Rightarrow x_1 = x_2 = 1 cr)

- Với (t = - 1 over 2). Ta có:

(eqalign & x^2 - 2rmx = - 1 over 2 Leftrightarrow 2rmx^2 - 4rmx + 1 = 0 cr & Delta ' = left( - 2 right)^2 - 2.1 = 4 - 2 = 2 cr & sqrt Delta ' = sqrt 2 cr & Rightarrow x_3 = - left( - 2 right) + sqrt 2 over 2 = 2 + sqrt 2 over 2 cr

& x_4 = - left( - 2 right) - sqrt 2 over 2 = 2 - sqrt 2 over 2 cr )

Vậy phương trình có 4 nghiệm: (x_1 = x_2 = 1;x_3 = 2 + sqrt 2 over 2;x_4 = 2 - sqrt 2 over 2)

b) (left( x + 1 over x right)^2 - 4left( x + 1 over x right) + 3 = 0)

Đặt (x + 1 over x = t) ta có phương trình: (t^2 – 4t + 3t = 0)

Phương trình có (a + b + c = 1 – 4 + 3 =0) nên có 2 nghiệm (t_1 =1, t_2=3)

Với (t_1 =1), ta có:

(eqalign & x + 1 over x = 1 cr & Leftrightarrow x^2 - x + 1 = 0 cr

& Delta = left( - 1 right)^2 - 4 = - 3 < 0 cr )

Phương trình vô nghiệm

Với (t_2= 3), ta có

(eqalign & x + 1 over x = 3 cr & Leftrightarrow x^2 - 3rmx + 1 = 0 cr & Delta = left( - 3 right)^2 - 4 = 5 cr

& Rightarrow x_1 = 3 + sqrt 5 over 2;x_2 = 3 - sqrt 5 over 2(TM) cr )

Vậy phương trình có 2 nghiệm: ( Rightarrow x_1 = 3 + sqrt 5 over 2;x_2 = 3 - sqrt 5 over 2)

Bài 60 trang 64 SGK Toán 9 tập 2

Bài 60. Với mỗi phương trình sau, đã biết một nghiệm (ghi kèm theo), hãy tìm nghiệm kia:

a) (12rmx^2 - 8rmx + 1 = 0;x_1 = 1 over 2)

b) (2rmx^2 - 7rmx - 39 = 0;x_1 = - 3)

c) (x^2 + x - 2 + sqrt 2 = 0;x_1 = - sqrt 2 )

d) (x^2 - 2mrmx + m - 1 = 0;x_1 = 2)

Hướng dẫn làm bài:

a) (12rmx^2 - 8rmx + 1 = 0;x_1 = 1 over 2)

Ta có: (x_1x_2 = 1 over 12 Leftrightarrow 1 over 2x_2 = 1 over 12 Leftrightarrow x_2 = 1 over 6)

b) (2rmx^2 - 7rmx - 39 = 0;x_1 = - 3)

Ta có: (x_1.x_2 = - 39 over 2 Leftrightarrow - 3rmx_2 = - 39 over 2 Leftrightarrow x_2 = 13 over 2)

c) (x^2 + x - 2 + sqrt 2 = 0;x_1 = - sqrt 2 )

Ta có:

(eqalign & x_1.x_2 = sqrt 2 - 2 cr & Leftrightarrow - sqrt 2 .x_2 = sqrt 2 - 2 cr

& Leftrightarrow x_2 = sqrt 2 - 2 over - sqrt 2 = sqrt 2 left( 1 - sqrt 2 right) over - sqrt 2 = sqrt 2 - 1 cr )

d) (x^2 - 2mrmx + m - 1 = 0;x_1 = 2)

Vì (x_1 = 2) là một nghiệm của pt (1) nên

(2^2- 2m.2 + m - 1 = 0)

(⇔ m = 1)

Khi (m = 1) ta có: (x_1x_2 = m - 1) (hệ thức Vi-ét)

(⇔ 2.x_2= 0) (vì (x_1 = 2) và (m = 1))

(⇔ x_2= 0)

Giaibaitap.me

Page 10

Bài 61 trang 64 SGK Toán 9 tập 2

Bài 61. Tìm hai số u và v trong mỗi trường hợp sau:

a) (u + v = 12); (uv = 28) và (u > v)

b) (u + v = 3; uv = 6)

Hướng dẫn làm bài:

a) (u + v = 12; uv = 28) và (u > v)

(u) và (v) là hai nghiệm của phương trình:

(x^2 – 12x + 28 = 0)

(Delta'= 36 – 28 = 8)

( Rightarrow x_1 = 6 + 2sqrt 2 ;x_2 = 6 - 2sqrt 2 )

Vì (6 + 2sqrt 2 > 6 - 2sqrt 2) nên suy ra (u = 6 + 2sqrt 2 ;v = 6 - 2sqrt 2)

b) (u + v = 3; uv = 6)

(u) và (v) là hai nghiệm của phương trình:

(x^2 – 3x + 6 = 0)

(Delta = (-3)^2 – 4.1.6 = 9 – 24 = -15 < 0)

Phương trình vô nghiêmh suy ra không còn 2 số (u) và (v) thỏa mãn điều kiện đã cho.

Bài 62 trang 64 SGK Toán 9 tập 2

Bài 62. Cho phương trình (7x^2 + 2(m – 1)x – m^2= 0)

a) Với giá trị nào của (m) thì phương trình có nghiệm?

b) Trong trường hợp phương trình có nghiệm, dùng hệ thức Vi-ét, hãy tính tổng những bình phương hai nghiệm của phương trình theo (m).

Giải

Xét phương trình (7x^2 + 2(m – 1)x – m^2 = 0) (1)

a) Phương trình có nghiệm khi (Delta’ ≥ 0)

Ta có: (Delta’ = (m – 1)^2 – 7(-m^2) = (m – 1)^2 + 7m^2 ≥ 0) với mọi (m)

Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của (m)

b) Gọi (x_1,x_2) là hai nghiệm của phương trình (1)

Ta có:

(eqalign & x_1^2 + x_2^2 = left( x_1 + x_2 right)^2 - 2rmx_1x_2 cr & = left[ - 2left( m - 1 right)^2 over 7 right] - 2 - m ^2 over 7 cr & = 4m^2 - 8m + 4 over 49 + 2m^2 over 7 cr & = 4m^2 - 8m + 4 + 14m^2 over 49 cr

& = 18m^2 - 8m + 4 over 49 cr )

Vậy (x_1^2 + x_2^2 = 18m^2 - 8m + 4 over 49) .

Bài 63 trang 64 SGK Toán 9 tập 2

Bài 63. Sau hai năm, số dân của một thành phố tăng từ 2 000 000 người lên 2 020 050 người. Hỏi trung bình mỗi năm dân số của thành phố đó tăng bao nhiêu phần trăm?

Giải

Gọi tỉ số tăng dân số trung bình mỗi năm là (x) % ((x > 0)).

Sau một năm dân số của thành phố là:

(2 000 000 + 2 000 000 . x over 100= 2 000 000 + 20 000x) (người)

Sau hai năm, dân số của thành phố là:

(2000000 +20 000x + (2000 000 + 20 000x). x over 100)

(= 2000 000 + 40 000x + 200x^2) (người)

Ta có phương trình:

(2 000 000 + 40 000x + 200x^2= 2 020 050)

(⇔ 4x^2 + 800x – 401 = 0)

(Delta' = 400^2 – 4(-401) = 160 000 + 1 604)

(= 161 604 > 0)

(sqrtDelta'= sqrt161 604 = 402)

Vậy phương trình có 2 nghiệm:

(x_1 = - 400 + 402 over 4 = 0,5(TM))

(x_2 = - 400 - 402 over 4 = - 200,5 < 0) (loại)

Tỉ lệ tăng dẫn số trung bình thường niên của thành phố là (0,5) %

Giaibaitap.me

Page 11

Bài 64 trang 64 SGK Toán 9 tập 2

Bài 64. Bài toán yêu cầu tìm tích của một số trong những dương với một số trong những to hơn nó 2 đơn vị, nhưng bạn Quân nhầm đầu bài lại tính tích của một số trong những dương với một số trong những bé nhiều hơn nữa nó 2 đơn vị. Kết quả của bạn Quân là 120. Hỏi nếu làm đúng đầu bài đã cho thì kết quả phải là bao nhiêu?

Giải:

Gọi (x) là số dương mà đấu bài cho, (x ∈ N*)

Bạn Quân đã chọn số ((x – 2)) để nhân với (x).

Theo đề bài, ta có: (x(x – 2) = 120) hay (x^2 – 2x – 120 = 0)

Giải phương trình ta được (x = 12) (thỏa mãn) và (x=-10) (loại)

Theo đầu bài yêu cầu tìm tích của (x) với (x +2)

Vậy kết quả đúng phải là: (12.14 = 168)

Bài 65 trang 64 SGK Toán 9 tập 2

Bài 65. Một xe lửa đi từ Tp Hà Nội Thủ Đô vào Bình Sơn (Tỉnh Quảng Ngãi). Sau đó 1 giờ, một xe lửa khác đi từ Bình Sơn ra Tp Hà Nội Thủ Đô với vận tốc to hơn vận tốc của xe lửa thứ nhất là 5km/h. Hai xe gặp nhau tại một ga ở ở chính giữa quãng đường Tp Hà Nội Thủ Đô – Bình Sơn dài 900km.

Giải:

Gọi (x) (km/h) là vận tốc của xe thứ nhất. Điều kiện (x > 0).

Khi đó vận tốc của xe lửa thứ hai là (x + 5) (km/h).

Thời gian xe lửa thứ nhất đi từ Tp Hà Nội Thủ Đô đến chỗ gặp nhau là: (450 over x) (giờ)

Thời gian xe lửa thứ hai đi từ Bình Sơn đến chỗ gặp nhau là: (450 over x + 5) (giờ)

Vì xe lửa thứ hai đi sau (1) giờ, nghĩa là thời gian đi đến chỗ gặp nhau ít hơn xe thứ nhất (1) giờ. Ta có phương trình:

(450 over x - 450 over x + 5 = 1 Leftrightarrow x^2 + 5rmx - 2250 = 0)

Giải phương trình ta được: (x_1 = 45) (nhận); (x_2 = -50) (loại)

Vậy: Vận tốc của xe lửa thứ nhất là (45) km/h

Vận tốc của xe lửa thứ hai là (50) km/h.

Bài 66 trang 64 SGK Toán 9 tập 2

Bài 66. Cho tam giác ABC có BC = 16cm , đường cao AH = 12 cm. Một hình chữ nhật MNPQ có đỉnh M thuộc cạnh AB, đỉnh N thuộc cạnh AC còn hai đỉnh P và Q. thuộc cạnh BC (h.17). Xác định vị trí của điểm M trên cạnh AB sao cho diện tích s quy hoạnh của hình chữ nhật đó bằng 36cm2.

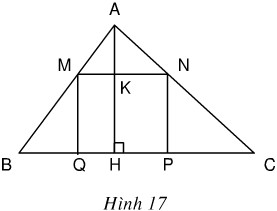
Giải:

Gọi (x) (cm) là độ dài của đoạn (AK). Điều kiện (0 < x < 12)

Vì (∆ABC) đồng dạng (∆AMN) nên

(eqalign & MN over BC = AM over AB = AK over AH = x over 12 cr

& Rightarrow MN = 16x over 12 = 4rmx over 3 cr )

Ta có: (MQ = KH = 12 – x)

Do đó diện tich hình chữ nhật (MNPQ) là: (left( 12 - x right)4rmx over 3)

Ta có phương trình:

(left( 12 - x right)4rmx over 3 = 36 Leftrightarrow x^2 - 12rmx + 27 = 0)

Giải phương trình ta được:

(x_1 = 9) (nhận) hoặc (x_2 = 3) (nhận)

Vậy độ dài của đoạn (AK = 3cm) hoặc (9cm). Khi đó (M) sẽ có hai vị trí trên (AB) nhưng diện tích s quy hoạnh hình chữ nhật (MNPQ) luôn bằng (36) cm2

Giaibaitap.me

Page 12

Giải bài 42, 43, 44, 45 trang 130, 131 SGK Toán 9... Giải bài 38, 39, 40, 41 trang 129 SGK Toán 9 tập 2 Giải bài 34, 35, 36, 37 trang 125,126 SGK toán 9... Giải bài 30, 31, 32, 33 trang 124, 125 SGK toán 9... Giải bài 27, 28, 29 trang 119, 120 SGK toán 9 tập... Giải bài 23, 24, 25, 26 trang 119 SGK toán 9 tập 2 Giải bài 19, 20, 21, 22 trang 118 SGK toán 9 tập 2 Giải bài 15, 16, 17, 18 trang 117 SGK toán 9 tập 2 Giải bài 12, 13, 14 trang 112, 113 SGK toán 9 tập... Giải bài 9, 10, 11 trang 112 SGK toán 9 tập 2

Page 13

Page 14

Bài 7 trang 69 sgk Toán lớp 9 tập 2

Bài 7. Cho hai tuyến đường tròn cùng tâm (O) với bán kính rất khác nhau. Hai đường thẳng đi qua (O) cắt hai tuyến đường tròn đó tại những điểm (A, B, C, D, M, N, P, Q.) (h.8)

a)Em có nhận xét gì về số đo của những cung (AM, CP, BN, DQ).

b) Hãy nêu tên những cung nhỏ bằng nhau.

c) Hãy nêu tên hai cung lớn bằng nhau.

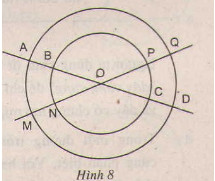
Hướng dẫn giải:

a) Các cung nhỏ (overparenAM, overparenCP, overparenBN, overparenDQ) có cùng số đo

b) (overparenAM) = (overparenDQ); (overparenBN) = (overparenPC); (overparenAQ) =(overparen MD); (overparenBP) =(overparenNC).

c) Các cung lớn bằng nhau:

(overparenAMDQ = overparenMAQD); (overparenBNCP = overparenNBPC);

Bài 8 trang 70 sgk Toán lớp 9 tập 2

Bài 8. Mỗi xác định sau đây đúng hay sai? Vì sao?

a) Hai cung bằng nhau thì có số đo bằng nhau.

b) Hai cung có số đo bằng nhau thì bằng nhau.

c) Trong hai cung, cung nào có số đo to hơn là cung to hơn.

d) Trong hai cung trên một đường tròn, cung nào có số đo nhỏ hơn thì nhỏ hơn.

Hướng dẫn giải:

a) Đúng

b) Sai. Không rõ hai cung nằm trên một đường tròn hay trên hai tuyến đường tròn bằng nhau không.

c) Sai( như trên)

d) Đúng

Bài 9 trang 70 sgk Toán lớp 9 tập 2

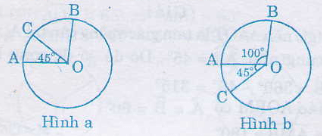
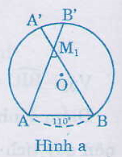
Bài 9. Trên đường tròn tâm (O) lấy ba điểm (A, B, C) sao cho (widehatAOB = 100^0), sđ cung (overparenAC = 45^0). Tính số đo của cung nhỏ (overparenBC) và cung lớn (overparenBC). (Xét cả hai trường hợp: điểm (C) nằm trên cung nhỏ (overparenAB), điểm (C) nằm trên cung lớn (overparenAB)).

Hướng dẫn giải:

a) Điểm (C) nằm trên cung nhỏ (overparenAB) ( hình a)

Số đo cung nhỏ (overparenBC = 100^0 – 45^0 = 55^0)

Số đo cung lớn (overparenBC = 360^0 – 55^0 = 305^0)

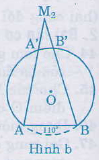
b) Điểm (C) nằm trên cung lớn (overparenAB) (hình b)

Số đo cung nhỏ (overparenBC = 100^0 + 45^0= 145^0)

Số đo cung lớn (overparenBC = 360^0 – 145^0 = 215^0)

Giaibaitap.me

Page 15

Bài 10 trang 71 sgk Toán lớp 9 tập 2

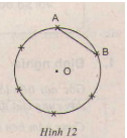
Bài 10. a) Vẽ đường tròn tâm (O) bán kinh (R = 2) cm. Nêu cách vẽ cung (overparenAB) có số đo bằng (60^0). Hỏi dây (AB) dài bao nhiêu xentimet?

b) Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như trên hình 12.

Hướng dẫn giải:

a) Vẽ đường tròn ((O; R)). Vẽ góc ở tâm có số đo (60^0). Góc này chắn (overparenAB) có số đo (60^0) (hình a).

Tam giác (AOB) cân có (widehatO=60^0) nên tam giác đều, suy ra (AB = R).

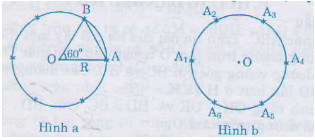
b) Theo câu a, ta có góc ở tâm bằng (sđoverparenAB=60^0). Số đo góc ở tâm vẽ được theo cách này là (360^0:60^0= 6). Suy ra được (6) cung tròn bằng nhau trên đường tròn.

Từ đó suy ra cách vẽ như sau:

Vẽ (6) dây cung bằng nhau và bằng bán kính (R):

(overparenA_1A_2 = overparenA_2A_3 = overparenA_3A_4= overparenA_4A_5 = overparenA_5A_6 = overparenA_6A_1)

(= rm R)

Từ đó suy ra (6) cung bằng nhau. (hình b)

Bài 11 trang 72 sgk Toán lớp 9 tập 2

Bài 11. Cho hai tuyến đường tròn bằng nhau ((O)) và ((O')) cắt nhau tại hai điểm (A) và (B). Kẻ những đường kính (AOC, AO'D). Gọi (E) là giao điểm thứ hai của (AC) với đường tròn ((O')).

a) So sánh những cung nhỏ (overparenBC, overparenBD).

b) Chứng minh rằng (B) là vấn đề ở chính giữa của cung (overparenEBD) ( tức điểm (B) chia cung (overparenEBD) thành hai cung bằng nhau: (overparenBE) = (overparenBD) ).

Hướng dẫn giải:

a) Nối (C) đến (D).

Ta có 2 đường tròn bằng nhau (=> AC = AD)

(=> ∆ ACD) cân tại (A)

Lại có (widehatABC = 90^0); do có (OB = OC = OA = R) ( tính chất trung tuyến ứng với cạnh huyền )

Tương tự có (widehatABD = 90^0)

(=> widehatABC + widehatABD = 180^0)

(=> C; B; D) thẳng hàng và (AB bot CD)

(=> BC = BD)

=> (overparenBC) = (overparenBD)

b) Nối (E) đến (D); từ (B) hạ (BH bot ED) Ta có góc (widehatDEA = 90^0) ( chứng tỏ tương tự theo (a) )

(=> BH // EC)

Mà theo (a) ta có (BE = BD)

(=> BH) là đường trung bình tam giác (CDE)

(=> HE = HD) mà (BH bot ED => B) là vấn đề ở chính giữa (overparenEBD)

Bài 12 trang 72 sgk Toán lớp 9 tập 2

Bài 12. Cho tam giác (ABC). Trên tia đối của tia (AB) lấy một điểm (D) sao cho (AD = AC). Vẽ đường tròn tâm (O) ngoại tiếp tam giác (DBC). Từ (O) lần lượt hạ những đường vuông góc (OH), (OK) với (BC) và (BD) ((H in BC, K in BD)).

a) Chứng minh rằng (OH > OK).

b) So sánh hai cung nhỏ (overparenBD) và (overparenBC).

Hướng dẫn giải:

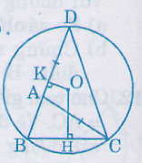
a) Trong (∆ABC), có (BC < BA + AC).

Mà (AC = AD) suy ra (BC < BD).

Theo định lí về dây cung và khoảng chừng cách từ dây đến tâm, ta có (OH > OK).

b) Ta có (BC < BD) (cmt)

nên suy ra (overparenBC) nhỏ hơn (overparenBD) ( liên hệ cung và dây)

Giaibaitap.me

Page 16

Bài 13 trang 72 sgk Toán lớp 9 tập 2

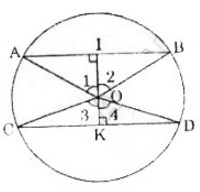
Bài 13. Chứng minh rằng trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.

Hướng dẫn giải:

Giả sử (AB) và (CD) là những dây song song của đường tròn ((O)).

Kẻ (OI bot AB) ((I in AB)) và (OK bot CD (Kin CD)).

Do (AB //CD) nên (I,O,K) thẳng hàng.

Do những tam giác (OAB, OCD) là những tam giác cân đỉnh (O) nên những đường cao kẻ từ đỉnh đồng thời là phân giác.

Vì vậy ta có: (widehat O_1 = widehat O_2 = widehat O_3 = widehat O_4)

Giả sử (AB) nằm ngoài (widehatCOD), ta có: (widehat AOC = 180^0 - widehat O_1 - widehat O_3 = 180^0 - widehat O_2 - widehat O_4 = widehat BOD)

Suy ra (overparenAC)= (overparenBD).

Nghĩa là hai cung bị chắn giữa hai dây song song thì bằng nhau. Các trường hợp khác ta chứng tỏ tương tự.

Bài 14 trang 72 sgk Toán lớp 9 tập 2

Bài 14

a) Chứng minh rằng đường kính đi qua điểm ở chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy. Mệnh đề đảo có đúng không? Hãy nêu thêm điều kiện để mệnh đề đảo đúng.

b) Chứng minh rằng đường kính đi qua điểm ở chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại

Hướng dẫn giải:

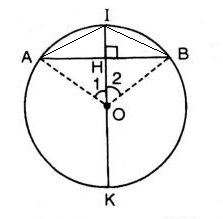
a. Vì (I) là vấn đề ở chính giữa của (overparenAB), suy ra (overparenIA) = (overparenIB) (⇒ IA = IB)

Ta có: (OA = OB =) bán kính. Suy ra đường kính (IK) là đường trung trực của dây (AB). Vậy (HA = HB) (đpcm)

Mệnh đề đảo: Đường kính đi qua trung điểm của một dây thì đi qua điểm ở chính giữa của cung căng dây đó.

Chứng minh: Vì (∆ AOB) cân tại (O) và (HA = HB) nên (OH) là đường phân giác của góc (widehatAOB). Suy ra (widehat O_1 = widehat O_2)

Từ đó suy ra (overparenIA) = (overparenIB)

Tuy nhiên điều này sẽ không thể xảy ra khi dây (AB) đi qua tâm (O) của đường tròn. Vậy phải thêm điều kiện để mệnh đề đảo đúng là:

Đường kính đi qua trung điểm của một dây không đi qua tâm thì đi qua điểm ở chính giữa của cung căng dây đó.

b. Ta có: (overparenIA) = (overparenIB) (gt) (⇒ IA = IB)

Điều này chứng tỏ rằng điểm ( I) nằm trên đường trung trực của (AB) (1)

Ta có (OA = OB =) bán kính

Điều này chứng tỏ rằng điểm (O) nằm trên đường trung trực của (AB) (2)

Từ (1) và (2) chứng tỏ rằng (OI) hay (IK) là đường trung trực của dây (AB). Suy ra (IK bot AB).

* Điều ngược lại: Đường kính vuông góc ở dây khi qua tâm thì đi qua hai điểm ở chính giữa của cung căng dây đó.

Kẻ đường kính (KOI) vuông góc với (AB).

Ta có (OA = OB ⇒ ∆OAB) cân tại (O)

Mà (OH bot AB) nên (OH) là đường phân giác của (widehatAOB) suy ra (widehat O_1 = widehat O_2)

Ta có (∆OAI = ∆OBI) (c.g.c). Do đó (AI = IB). Suy ra (overparenAI) = (overparenIB).

Vậy (I) là vấn đề ở chính giữa của (overparenAB)

Giaibaitap.me

Page 17

Page 18

Bài 19 trang 75 sgk Toán lớp 9 tập 2

Bài 19. Cho một đường tròn tâm (O), đường kính (AB) và (S) là một điểm nằm ngoài đường tròn. (SA) và (SB) lần lượt cắt đường tròn tại (M, N). Gọi (H) là giao điểm của (BM) và (AN). Chứng minh rằng (SH) vuông góc với (AB).

Hướng dẫn giải:

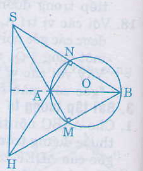
(BM bot SA) ((widehatAMB) = (90^circ) vì là góc nội tiếp chắn nửa đường tròn).

Tương tự, có: (AN bot SB)

Như vậy (BM) và (AN) là hai tuyến đường cao của tam giác (SAB) và (H) là trực tâm.

Suy ra (SH bot AB).

(Trong một tam giác ba đường cao đồng quy)

Bài 20 trang 76 sgk Toán lớp 9 tập 2

Bài 20. Cho hai tuyến đường tròn ((O)) và ((O')) cắt nhau tại (A) và (B). Vẽ những đường kính (AC) và (AD) của hai tuyến đường tròn. Chứng minh rằng ba điểm (C, B, D) thẳng hàng.

Hướng dẫn giải:

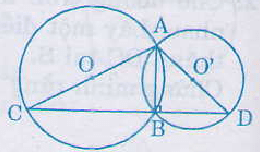
Nối (B) với 3 điểm (A, C, D) ta có:

(widehatABC) = (90^circ)

(góc nội tiếp chắn nửa đường tròn)

(widehatABD) =(90^circ)

( góc nội tiếp chắn nửa đường tròn)

Vậy (widehatABC) + (widehatABD) = (180^circ)

Suy ra ba điểm (A, C, D) thẳng hàng.

Bài 21 trang 76 sgk Toán lớp 9 tập 2

Bài 21. Cho hai tuyến đường tròn bằng nhau ((O)) và ((O')) cắt nhau tại (A) và (B). Vẽ đường thẳng qua (A) cắt (O) tại (M) và cắt ((O')) tại (N) ( (A) nằm giữa (M) và (N)). Hỏi (MBN) là tam giác gi? Tại sao?

Hướng dẫn giải:

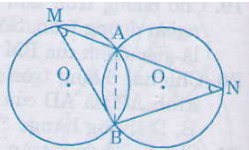
Do hai tuyến đường tròn bằng nhau nên hai cung nhỏ (overparenAB) bằng nhau. Vì cùng căng dây (AB).

Suy ra (widehat N = widehat M) (cùng chắn hai cung bằng nhau) nên tam giác (BMN) là tam giác cân đỉnh (B)

Bài 22 trang 76 sgk Toán lớp 9 tập 2

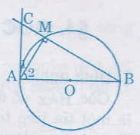
Bài 22. Trên đường tròn ((O)) đường kính (AB), lấy điểm (M) (khác (A) và (B)). Vẽ đường qua (A) cắt ((O)) tại (A). Đường thẳng (BM) cắt tiếp tuyến đó tại (C). Chứng minh rằng ta luôn có: (MA^2 = MB.MC)

Hướng dẫn giải:

Ta có: (∆MAB) đồng dạng (∆MCA) ((widehatA_2) = (widehatC); (widehatB) = (widehatA_1))

nên (fracMAMB) = (fracMCMA)

Suy ra (MA^2 = MB.MC)

Giaibaitap.me

Page 19

Bài 23 trang 76 sgk Toán lớp 9 tập 2

Bài 23. Cho đường tròn ((O)) và một điểm (M) cố định và thắt chặt không nằm trên đường tròn. Qua (M) kẻ hai tuyến đường thẳng. Đường thẳng thứ nhất cắt ((O)) tại (A) và (B).Đường thẳng thứ nhất cắt ((O)) tại (C) và (D).

Chứng minh (MA. MB = MC. MD)

Hướng dẫn giải:

Xét hai trường hợp:

a) (M) ở bên trong đường tròn (hình a)

Xét hai tam giác (MAB') và (MA'B) có:

(widehatM_1) = (widehatM_2) ( đối đỉnh)

(widehatB') = (widehatB) (hai góc nội tiếp cùng chắn cung (AA')).

Do đó (∆MAB') đồng dạng (∆MA'B), suy ra:

(fracMAMA') = (fracMB'MB), do đó (MA. MB = MB'. MA')

b) (M ở bên phía ngoài đường tròn (hình b)

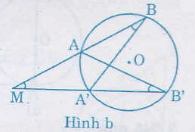
Tương tự ta có:

(∆MAB') đồng dạng (∆MA'B)

(widehatM) chung

(widehatB') = (widehatB) (hai góc nội tiếp cùng chắn cung (AA')).

Suy ra: (fracMAMA') = (fracMB'MB)

hay (MA. MB = MB'. MA')

Bài 24 trang 76 sgk Toán lớp 9 tập 2

Bài 24. Một chiếc cầu được thiết kế như hình 21 có độ dài (AB = 40)m, độ cao (MK = 3)m. Hãy tính bán kính của đường tròn chứa cung (AMB)

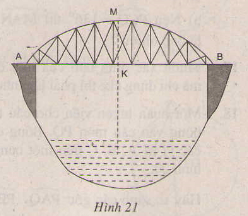
Hướng dẫn giải:

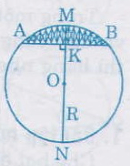
Gọi (MN = 2R) là đường kính của đường tròn có cung tròn là (AMB)

Theo bài tập 23, ta có:

(KA. KB = KM. KN)

hay (KA. KB = KM. (2R - KM))

Thay số, ta có:

(20. 20 = 3(2R - 3))

do đó (6R = 400 + 9 = 409).

Vậy (R) = (frac4096) (≈68,2) (mét)

Bài 25 trang 76 sgk Toán lớp 9 tập 2

Bài 25. Dựng một tam giác vuông, biết cạnh huyền dài (4)cm và một cạnh góc vuông dài (2,5) cm.

Hướng dẫn giải:

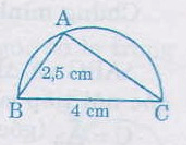
Cách vẽ như sau:

- Vẽ đoạn thẳng (BC) dài (4cm).

- Vẽ nửa đưởng tròn đường kính (BC).

- Vẽ dây (AB) (hoặc dây (CA)) dài (2,5cm).

Ta có tam giác thỏa mãn những yêu cầu của đầu bài ( (widehatA)=(90^circ), (BC = 4cm, AB = 2,5cm))

Bài 26 trang 76 sgk Toán lớp 9 tập 2

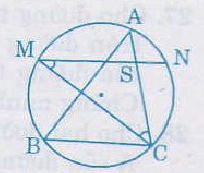
Bài 26. Cho (AB, BC, CA ) là ba dây của đường tròn ((O)). Từ điểm ở chính giữa (M) của (overparenAB) vẽ dây (MN) song song với dây (BC). Gọi giao điểm của (MN) và (AC) là (S). Chứng minh (SM = SC) và (SN = SA)

Hướng dẫn giải:

Ta có:

(overparenMA)= (overparenMB) (theo gt).

(overparenNC)= (overparenMB) ( vì (MN // BC))

Suy ra (overparenMA) = (overparenNC), do đó (widehat ACM = widehat CMN)

Vậy (∆SMC) là tam giác cân, suy ra (SM = SC)

Chứng minh tương tự ta cũng luôn có thể có (∆SAN) cân , (SN = SA).

Giaibaitap.me

Page 20

Page 21

Page 22

Page 23

Bài 36 trang 82 sgk Toán lớp 9 tập 2

Bài 36. Cho đường tròn ((O)) và hai dây (AB), (AC). Gọi (M, N) lần lượt là vấn đề ở chính giữa của cung (AB) và cung (AC). Đường thẳng (MN) cắt dây (AB) tại (E) và cắt dây (AC) tại (H). Chứng minh rằng tam giác (AEH) là tam giác cân.

Hướng dẫn giải:

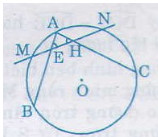
Ta có: (widehat AHM)= (fracsđoverparenAM+sđoverparenNC2) (1)

(widehat AEN)= (fracsđoverparenMB+sđoverparenAN2) (2)

(Vì widehat AHM)và (widehat AEN)là những góc có đỉnh cố định và thắt chặt ở bên trong đường tròn).

Theo gỉả thiết thì:

(overparenAM=overparenMB (3))

(overparenNC=overparenAN (4))

Từ (1),(2), (3), (4), suy ra (widehat AHM)= (widehat AEN) do đó (∆AEH) là tam giác cân.

Bài 37 trang 82 sgk Toán lớp 9 tập 2

Bài 37. Cho đường tròn ((O)) và hai dây (AB), (AC) bằng nhau. Trên cung nhỏ (AC) lấy một điểm (M). Gọi (S) là giao điểm của (AM) và (BC). Chứng minh: (widehat ASC)=(widehat MCA)

Hướng dẫn giải:

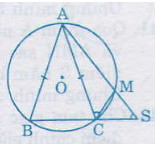
Ta có: (widehat ASC)= (fracsđoverparenAB+sđoverparenMC2) (1)

((widehat ASC) là góc có đỉnh nằm bên phía ngoài đường tròn ((O)))

và (widehat MCA)=(fracsđoverparenAM2) (2)

(góc nội tiếp chắn cung (overparenAM))

Theo giả thiết thì:

(AB = AC =>)(overparenAB=overparenAC) (3)

Từ (1), (2), (3) suy ra: (overparenAB-overparenMC=overparenAC-overparenMC=overparenAM)

Từ đó (widehat ASC=widehat MCA).

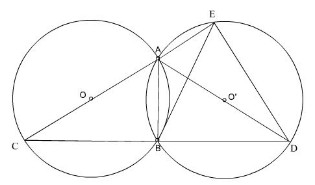
Bài 38 trang 82 sgk Toán lớp 9 tập 2

Bài 38. Trên một đường tròn, lấy liên tục ba cung (AC, CD, DB) sao cho

(sđoverparenAC)=(sđoverparenCD)=(sđoverparenDB)=(60^0). Hai đường thẳng (AC) và (BD) cắt nhau tại (E). Hai tiếp tuyến của đường tròn tại (B) và (C) cắt nhau tại (T). Chứng minh rằng:

a) (widehat AEB=widehat BTC);

b) (CD) là phân giác của (widehatBTC)

Hướng dẫn giải:

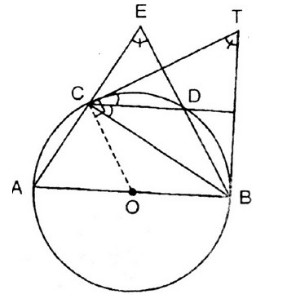
a) Ta có (widehatAEB) là góc có đỉnh ở bên phía ngoài đường tròn nên:

(widehatAEB)=(fracsđoverparenAB-sđoverparenCD2)=(180^0 - 60^0 over 2 = 60^0)

và (widehatBTC) cũng là góc có đỉnh ở bên phía ngoài đường tròn ( hai cạnh đều là tiếp tuyến của đường tròn) nên:

(widehatBTC)=(fracwidehat BAC-widehat BDC2)=((180^0 + 60^0) - (60^0 + 60^0) over 2 = 60^0)

Vậy (widehat AEB =widehat BTC)

b) (widehat DCT ) là góc tạo bởi tiếp tuyến và dây cung nên:

(widehat DCT=fracsđoverparenCD2)

(widehat DCB) là góc nội tiếp trên

(widehat DCB=fracsđoverparenDB2=60^0 over 2 = 30^0)

Vậy (widehat DCT=widehat DCB) hay (CD) là phân giác của (widehat BCT )

Bài 39 trang 83 sgk Toán lớp 9 tập 2

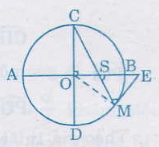
Bài 39. Cho (AB) và (CD) là hai tuyến đường kính vuông góc của đường tròn ((O)). Trên cung nhỏ (BD) lấy một điểm (M). Tiếp tuyến tại (M) cắt tia (AB) ở (E), đoạn thẳng (CM) cắt (AB) ở (S).Chứng minh (ES = EM).

Hướng dẫn giải:

Ta có (widehatMSE) = (fracsđoverparenCA+sđoverparenBM2) (1)

( vì (widehatMSE) là góc có đỉnh S ở trong đường tròn (O))

(widehatCME) = (fracsđoverparenCM2)= (fracsđoverparenCB+sđoverparenBM2) (2)

((widehatCME) là góc tạo bởi tiếp tuyến và dây cung).

Theo giả thiết (overparenCA=overparenCB) (3)

Từ (1), (2), (3) ta có: (widehatMSE) = (widehatCME) từ đó (∆ESM) là tam giác cân và (ES = EM)

Giaibaitap.me

Page 24

Bài 40 trang 83 sgk Toán lớp 9 tập 2

Bài 40. Qua điểm S nằm bên phía ngoài đường tròn (O), vẽ tiếp tuyến SA và cát tuyến SBC của đường tròn. Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD

Trả lời:

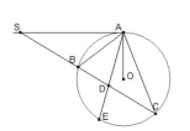
Có: (widehat ADS=fracsđoverparenAB-sđoverparenCE2) (định lí góc có đỉnh ở ngoài đường tròn).

(widehat SAD=frac12 sđoverparenAE) (định lí góc giữa tia tiếp tuyến và dây cung).

Có: (widehat BAE = widehat EAC) (Rightarrow ) (overparenBE=overparenEC)

(Rightarrow) (sđoverparenAB)+(sđoverparenEC)=(sđoverparenAB+sđoverparenBE)=

(sđoverparenAE)

nên (widehat ADS=widehat SAD)(Rightarrow) tam giác (SDA) cân tại (S) hay (SA=SD).

Bài 41 trang 83 sgk Toán lớp 9 tập 2

Bài 41. Qua điểm (A) nằm bên phía ngoài đường tròn ((O)) vẽ hai cát tuyến (ABC) và (AMN) sao cho hai tuyến đường thẳng (BN) và (CM) cắt nhau tại một điểm (S) nằm bên trong đường tròn.

Chứng minh:

(widehat A + widehat BrmSM = 2widehat CMN)

Hướng dẫn giải:

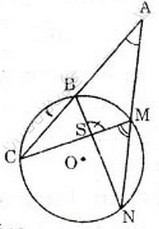
Ta có :

(widehatA)+(widehat BSM = 2widehat CMN)

(widehat A)=(fracsđoverparenCN-sđoverparenBM2) (góc (A) là góc ngoài ((0))) (1)

(widehat BSM)=(fracsđoverparenCN+sđoverparenBM2) (góc (S) là góc trong ((0))) (2)

(widehat CMN)=(fracsđoverparenCN2)

(Leftrightarrow) (2widehat CMN)=(sđoverparenCN). (3)

Cộng (1) và(2) theo vế với vế:

(widehatA)+(widehat BSM) =(frac2sđoverparenCN+(sđoverparenBM-sđoverparenBM)2)=(overparenCN)

Từ (3) và (4) ta được: (widehat A + widehat BrmSM = 2widehat CMN)

Bài 42 trang 83 sgk Toán lớp 9 tập 2

Bài 42. Cho tam giác (ABC) nội tiếp đường tròn. (P, Q., R) theo thứ tự là những điểm ở chính Một trong những cung bị chắn (BC, CA, AB) bởi những góc (A, B, C).

a) Chứng minh (AP bot QR)

b) (AP) cắt (CR) tại (I). Chứng minh tam giác (CPI) là tam giác cân

Hướng dẫn giải:

a) Gọi giao điểm của (AP) và (QR) là (K).

(widehatAKR) là góc có đỉnh ở bên trong đường tròn nên

(widehatAKR) = (fracsđoverparenAR+sđoverparenQC+sđoverparenCP2)=(fracsđoverparenAB+sđoverparenAC+sđoverparenBC4=90^0)

Vậy (widehatAKR = 90^0) hay (AP bot QR)

b) (widehatCIP) là góc có đỉnh ở bên trong đường tròn nên:

(widehatCIP) = (fracsđoverparenAR+sđoverparenCP2) (1)

(widehat PCI) góc nội tiếp, nên (widehat PCI)= (fracsđoverparenRB+sđoverparenBP2) (2)

Theo giả thiết thì cung (overparenAR = overparenRB) (3)

Cung (overparenCP = overparenBP) (4)

Từ (1), (2), (3), (4) suy ra: (widehat CIP=widehat PCI). Do đó (∆CPI) cân.

Bài 43 trang 83 sgk Toán lớp 9 tập 2

Bài 43. Cho đường tròn ((O)) và hai dây cung song song (AB, CD) ((A) và (C) nằm trong cùng một nửa mặt phẳng bờ (BD)); (AD) cắt (BC) tại (I)

Chứng minh (widehatAOC ) = (widehatAIC ).

Hướng dẫn giải:

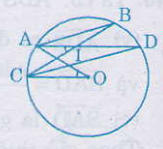
Theo giả thiết: (overparenAC)=(overparenBD) (vì (AB // CD)) (1)

(widehatAIC ) = (fracsđoverparenAC+sđoverparenBD2) (2)

Theo (1) suy ra (widehatAIC ) = (sđoverparenAC) (3)

(widehatAOC ) = (sđoverparenAC) (góc ở tâm chắn cung (overparenAC)) (4)

So sánh (3), (4), ta có (widehatAOC ) = (widehatAIC ).

Giaibaitap.me

Page 25

Page 26

Bài 47 trang 86 sgk Toán lớp 9 tập 2

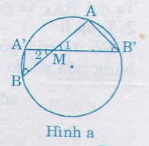
Bài 47. Gọi cung chứa góc (55^0) ở bài tập 46 là (overparenAmB). Lấy điểm (M_1) nằm bên trong và điểm (M_2) nằm bên phía ngoài đường tròn chứa cung này sao cho (M_1,M_2) và cung (overparenAmB) nằm cùng về một phía đối với đường thẳng (AB). Chứng minh rằng:

a) (widehat AM_1B > 55^0);

b) (widehat AM_2B < 55^0).

Hướng dẫn giải:

(M_1) là vấn đề bất kì nằm trong cung chứa góc (55^0) (hình a).

Gọi (B’, A’) theo thứ tự là giao điểm của (M_1A), (M_1B) với cung tròn. Vì (widehatAM_1B) là góc có đỉnh nằm trong đường tròn, nên: (widehat AM_1B) = (fracsđoverparenAB+sđoverparenA'B'2) = (55^0)+ (một số trong những dương).

Vậy (widehat AM_1B > 55^0)

(M_2) là vấn đề bất kì nằm ngoài đường tròn (h.b), (M_2A,M_2B) lần lượt cắt đường tròn tại (A’, B’.) Vì góc (widehat AM_2B) là góc có đỉnh nằm bên phía ngoài đường tròn nên:

(widehat AM_2B)=(fracsđoverparenAB-sđoverparenA'B'2)=(55^0)- (một số trong những dương)

Vậy (widehat AM_2B < 55^0)

Bài 48 trang 87 sgk Toán lớp 9 tập 2

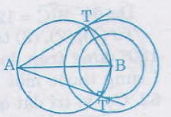
Bài 48. Cho hai điểm (A, B) cố định và thắt chặt. Từ (A) vẽ những tiếp tuyến với đường tròn tâm (B) bán kính không to hơn (AB). Tìm quỹ tích những tiếp điểm.

Hướng dẫn giải:

- Trường hợp những đường tròn tâm (B) có bán kính (BA). Tiếp tuyến (BA) vuông góc với bán kính (BT) tại tiếp điểm (T).

Do (AB) cố định và thắt chặt nên quỹ tích của (T) là đường tròn đường kính (AB).

- Trường hợp những đường tròn tâm (B) có bán kính to hơn (BA): quỹ tích là tập hợp rỗng.

Bài 49 trang 87 sgk Toán lớp 9 tập 2

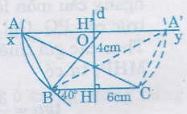
Bài 49. Dựng tam giác (ABC), biết (BC = 6cm), (widehatA) = (40^0) và đường cao (AH = 4cm).

Hướng dẫn giải:

Trình tự dựng gồm 3 bước:

- Dựng đoạn thẳng (BC = 6cm)

- Dựng cung chứa góc (40^0) trên đoạn thẳng (BC).

- Dựng đường thẳng (xy) song song với (BC) và cách (BC) một khoảng chừng là (4cm) như sau:

Trên đường trung trực (d) của đoạn thẳng (BC) lấy đoạn (HH' = 4cm) (dùng thước có chia khoảng chừng mm). Dựng đường thẳng (xy) vuông góc với (HH') tại (H).

Gọi giao điểm (xy) và cung chứa góc là (widehatA), (widehatA'). Khi đó tam giác (ABC) hoặc (A'BC) đều thỏa yêu cầu của đề toán

Giaibaitap.me

Review Giải bài 32 SGK Toán 9 tập 2 trang 54 ?

Bạn vừa đọc tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Review Giải bài 32 SGK Toán 9 tập 2 trang 54 tiên tiến nhất

Share Link Tải Giải bài 32 SGK Toán 9 tập 2 trang 54 miễn phí

Người Hùng đang tìm một số trong những Chia SẻLink Download Giải bài 32 SGK Toán 9 tập 2 trang 54 miễn phí.

Giải đáp thắc mắc về Giải bài 32 SGK Toán 9 tập 2 trang 54

Nếu sau khi đọc nội dung bài viết Giải bài 32 SGK Toán 9 tập 2 trang 54 vẫn chưa hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha #Giải #bài #SGK #Toán #tập #trang - 2022-07-14 01:10:07

Thù.vn News - Tut Apps Android

Table of Content

Giải bài 32 SGK Toán 9 tập 2 trang 54 ✅ Vip

Thủ Thuật về Giải bài 32 SGK Toán 9 tập 2 trang 54 Chi Tiết

Review Giải bài 32 SGK Toán 9 tập 2 trang 54 ?

Share Link Tải Giải bài 32 SGK Toán 9 tập 2 trang 54 miễn phí

Giải đáp thắc mắc về Giải bài 32 SGK Toán 9 tập 2 trang 54

Đăng nhận xét

thù.vn